Overview

In project 5 we create face morphs - smooth transitions from one face to another. We then use our morphing powers to morph a large data set of images into an average face. From this population mean we can compute the difference between an individual and the mean and extrapolate to create face caricatures.

The morphing process is not for the faint of heart! The four outside images above show various unsuccessful attempts at morphing. (Perhaps they are works of art in their own right?) In the center is the final result - Emma Watson morphed into Daniel Radcliffe.

Face Morphing

A morph is a smooth transition from one arrangement of points to a different arrangement of the same points. Linear morphs can be computed for any set of shapes that span a linear subspace. (A linear subspace is basically anything for which a quantitative, rather than qualitative, relationship exists. For example, coordinates span a linear subspace because there is a quantitative relationship between any two points. Traffic lights on the other hand do not span a linear subspace because a yellow signal has no quantitative relationship to a red signal or a green signal.)

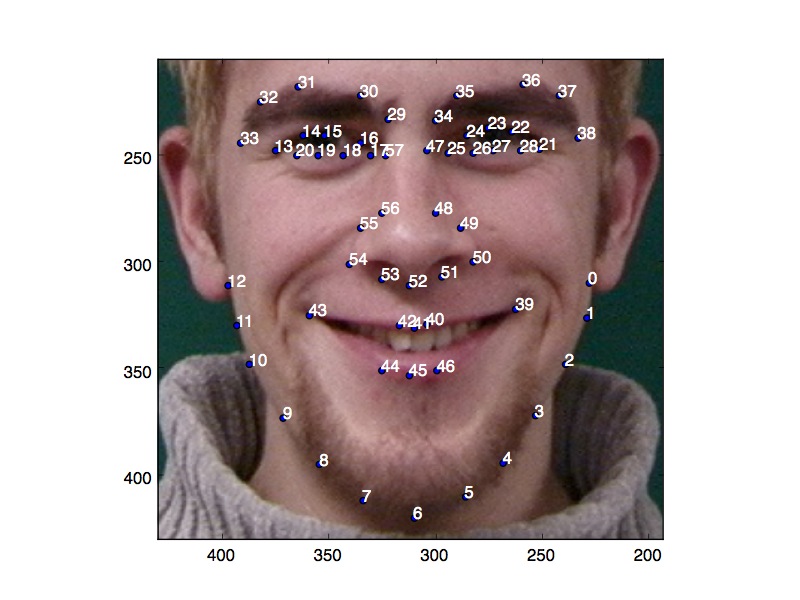
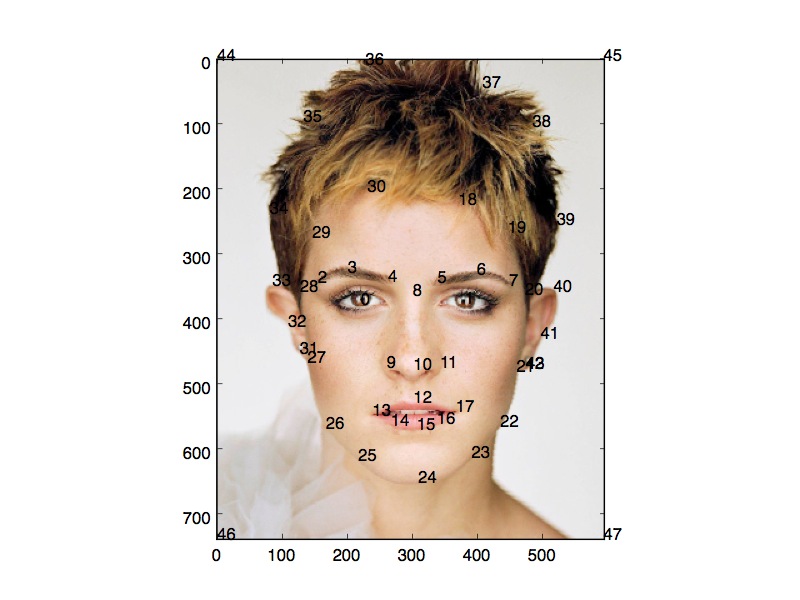
A crucial aspect of morphing is the selection of corresponding points. It is vital that the points correspond not to the same location in space, but rather to the same physical feature. For face morphing, we select features like the eyes, nose, jawline, and hairline to align the faces. The alignment is both tedious and unforgiving, especially around the eyes.

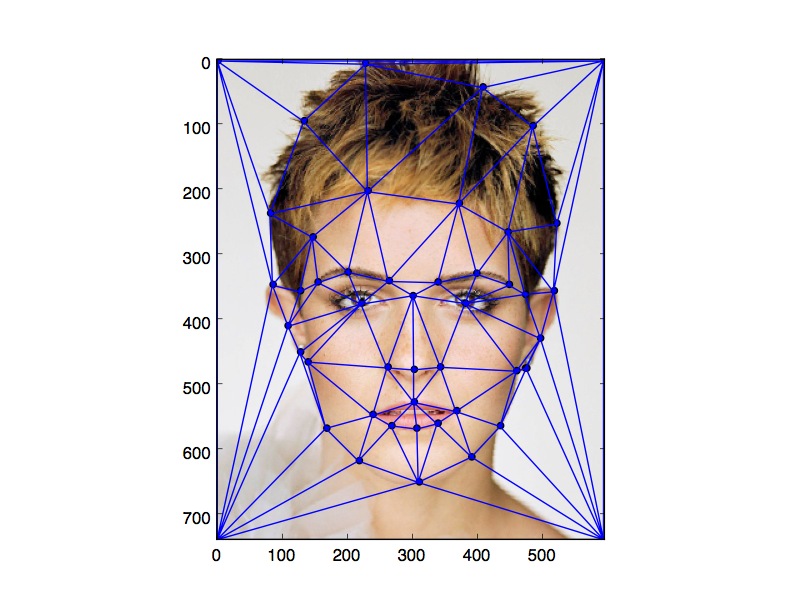
Below are two illustrations of the corresponding points used for this project, along with the Delaunay triangulation (described below).

Once we obtain the corresponding points for each face, we average the shape coordinates to obtain the average face shape. We then compute a Delaunay trianulation to parse the image into triangles. The Delaunay triangulation minimizes the number of triangles that span large regions, which helps prevent non-local warping.

Next, we compute the affine transformation matrix from the original shape (the source) to the average shape (the target). An affine transformation may include scaling, rotation, shearing, and translation. The transformation matrix is of the form:

[[a, b, tx]
 [c, d, ty]
  [0, 0,  1]]

where (tx, ty) is the translation vector and the points to be transformed (triangle vertices) are three column vectors:

[[x1, x2, x3]
 [y1, y2, y3]
  [ 1,  1,  1]]

I solved for the matrix by computing a 3x3 matrix, A, that satisfies the equation A p = p', where p is the target point and p' is the source point. I computed the transformation from target to source so that I did not need to worry about over- or under-sampling the target image.

As a side note, the method I used only iterates over each triangle rather than each pixel. For each triangle I find a mask of the coordinates inside the triangle and compute and apply the transformation all at once.

The transformation generally does not return integer pixel values, so some resampling to get the correct color value in the source image is necessary. I tried to implement a linear interpolation using the 4 neighbor of each pixel, but the debugging time was too great and I eventually gave up. Instead I settled for a simple rounding method to the nearest integer, which produces some visible artifacts. Alas, my time is finite.

To produce the final sequence, I simply calculate a linspace of weights given the number of frames, and for each frame I weight the two shapes, morph the faces, and weight the two images.

Average Faces

Using the method outlined above we can also compute the average of a population (given that we have corresponding points for each face). For this assignment I decided to use the IMM face database from the University of Denmark, consisting of 40 faces (33 men and 7 women), sans three which I discarded because they had been corrupted and were no longer in color. In addition to computing the average face from the IMM, I also obtained the average female face for various nationalities from a face averaging project conducted at the University of Glasgow. Shown below are the average female German, Finnish, and Irish faces (the three nationalities that best represent my genetic heritage), the average female American and the average female Mongolian (to which I am not at all related).

Caricatures

Since we know that face shapes span a subspace, we can extrapolate in different directions within the subspace to create caricatures. To create the caricature shape, we calculate the difference between the individual's face shape and the average face shape and either add or subtract that difference (times a multiplier - in this case 0.8) from the individual's face shape. We can then morph the individual into the caricature face shape. I decided to create both normal "forward" caricatures (moving the individual farther from the mean), as well as "backward" caricatures (moving the individual closer to the mean). I think this comparison makes it even easier to see the influence of the type of average used.

One problem that I encountered with the caricatures is that they are more sensitive to small errors in the position of corresponding points since any deviations are exaggerated. For this reason I had to re-select more consistent corresponding points in some cases.

For a bell & whistle I also morphed the average mongolian face to be more or less like my face (in other words, I used the appearance of the mongolian avg. and the shape of my face).

Other results

I decided to try computing the mean face of a smaller population. Shown below is the average of the four Beatles and caricatures to and from the average for each member. The average is not as clean because of slightly varying poses, but the caricatures worked pretty well!

I also made some continuous loop morphs by warping one face into another, then another, then back to the first face. Additionally, I made a non-face warp between three pokemon using corresponding points in the eyes and around the perimeter. The pokemon do not really span a linear subspace (their shapes are just too different), so there are a lot of warping artifacts and visible cross-fade. Finally, for my other bell & whistle I also participated in the class face warp.